The Analog Ensemble is a statistical technique that generates probabilistic forecasts using a current deterministic prediction, a set of historical predictions, and the associated observations. It is a computationally efficient solution for ensemble modeling because it does not require multiple numerical weather prediction simulations, but a single model realization.
Despite this intrinsic computational efficiency, the required computation can grow very large because atmospheric models are routinely run with increasing resolutions. For example, the North American Mesoscale forecast system contains over 262 792 grid points to generate a 12 km prediction. This project aims to propose an evolutionary algorithm which can dynamically and automatically learn the optimal unstructured grid pattern and construct the mesh based on the predefined metrics. This iterative evolutionary algorithm is guided by Darwinian evolutionary rule generation and instantiation to identify grid vertices. Analog computations are performed only at vertices. Therefore, minimizing the number of vertices and identifying their locations are paramount to optimizing the available computational resources, minimizing queue time, and ultimately achieving better results. The optimal unstructured grid is then reused to guide the predictions for a variety of applications like temperature and wind speed.
This project is funded by the NSF EarthCube office.
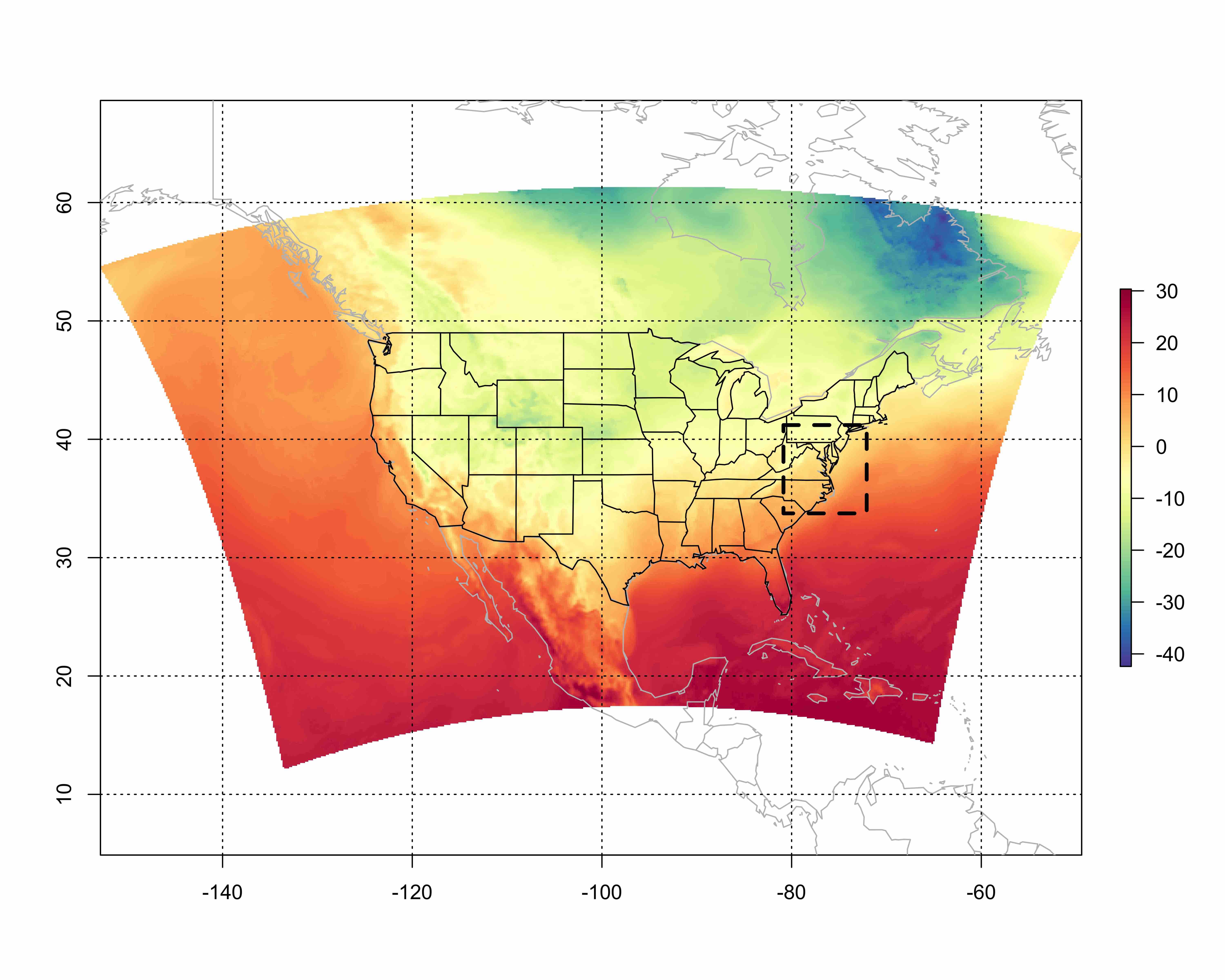
A temperature map from NAM model forecast at 3 AM on December 31, 2014, at 2 m above ground level. The black dashed rectangle shows the subset region with 4,424 grid points as the study area.
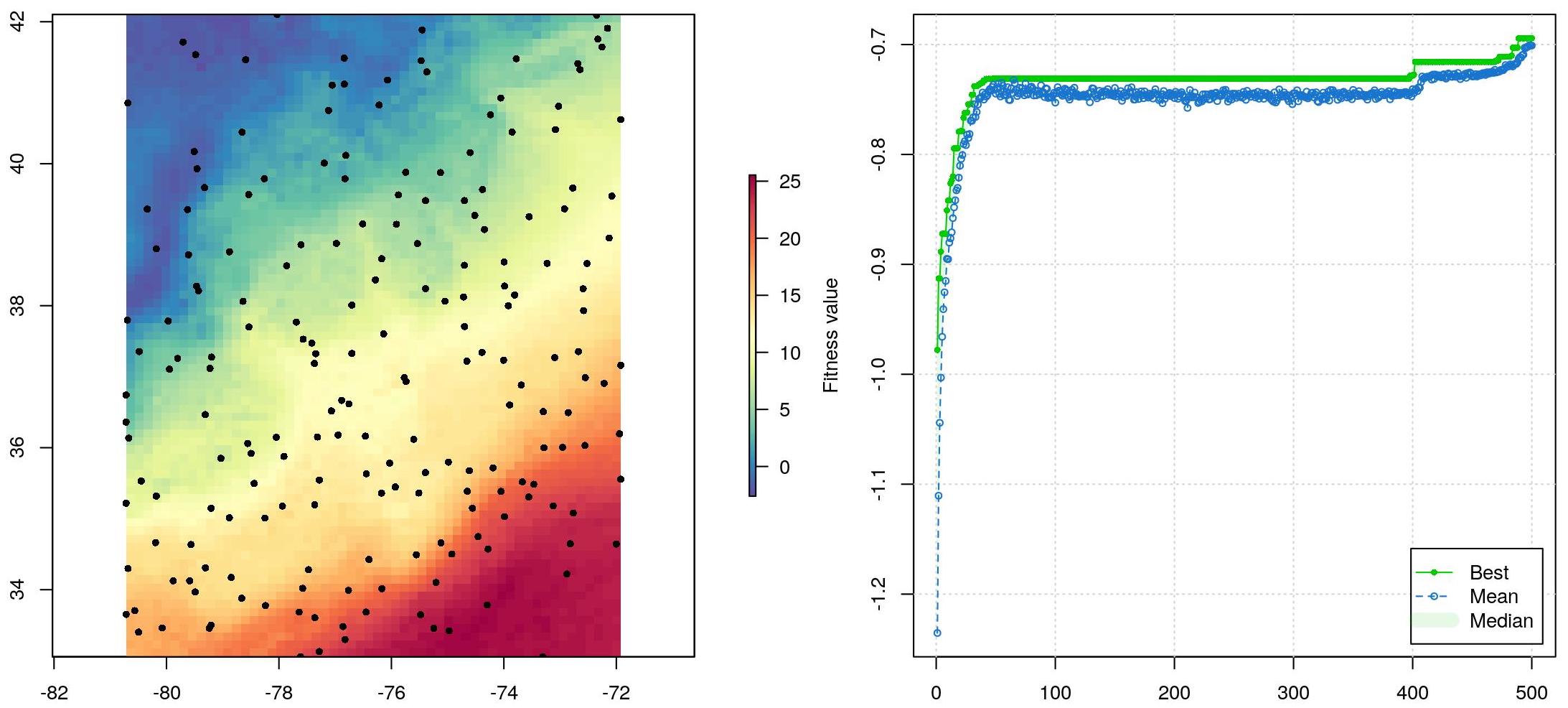
The left figure shows the best set of vertices from the generation population after 500 iterations. The right figure shows the evolution of fitness measures for each generation population.
The YouTube video demonstrates how this technique can be applied to a larger domain. The unstructured grid gradually adapts itself to the gradience of temperature changes. As a result, regions with higher temperature gradient ends up with a denser mesh.
An online poster for this project is also available at this post from Weiming.